У третьому класі школярі вперше стикаються з дробами, і часто це стає викликом для їхнього розуміння цієї теми. Операції віднімання і додавання дробів виглядають складнішими в порівнянні з конкретними задачами, які діти вирішували до цього. Незважаючи на це, розуміння дробів є ключовим етапом у вивченні математики, і важливо засвоїти це поняття, щоб уникнути відставання в майбутньому.
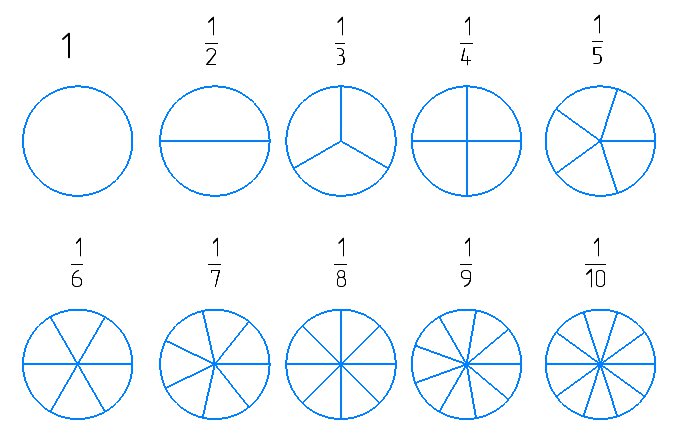
Що таке дроби?
Першу думку, яку батьки повинні передати дітям, полягає в тому, що дроби — це дещо таке ж невід'ємне в нашому житті, як таблиця множення чи завдання на находження швидкості і відстані. Це не складні числа чи заплутані вирази; це абсолютно реальні поняття, які можна знайти в будь-якому місці. Ось як можна оформити поняття дробів:
"Дріб — це засіб запису частини будь-якого предмету у цифровому вигляді. Якщо уявити, що одне яблуко дорівнює 1, то його половина буде виглядати як 1/2. Подумаймо про операцію ділення: спочатку ми ділимо яблуко на дві рівні частини, і одна з них стає його половиною. Таким чином, ми отримуємо 1/2".

Якщо розуміння дробів для вашої дитини виявляється важким завданням, а шкільні заняття не приносять достатньої допомоги, батьки можуть спробувати самостійно навчити свою дитину. Проте, найбільш ефективним методом для поліпшення успішності в школі залишається залучення репетиторів. Також ви можете скористатися ГДЗ математика 6 клас Істер.
З чого варто розпочати вивчення дробів
Спосіб розпочати вивчення дробів може бути нескладним і ефективним, якщо використовувати реальні предмети для їхнього ілюстрування. Це може бути яблуко, торт, цукерка, кубики чи лего. Рекомендуємо почати з пояснення дробів на прикладі 1/2 та 1/3, оскільки ці прості вирази легко зобразити і записати. Це основні ідеї, які важливо донести в самому початку.
Що ж таке чисельник і знаменник в дробах?
У дробу є два важливих елементи: верхнє та нижнє число. Верхнє число зветься "чисельником", а число під ним – "знаменником". Знаменник вказує на кількість частин, на які поділено яблуко, тоді як чисельник показує, скільки з цих частин ви вже маєте.
Якщо знаменник і чисельник – це одне і те саме число, то значення дробу дорівнює одиниці.
Візьміть печиво і розділіть його на чотири однакові частини, показуючи дитині: "Отже, це печиво ми розділили на 4 рівні частини. Всі вони тепер у тебе. Ти вже маєш всі частини, отже, ти володієш цілим печивом. Це саме те, що ми позначаємо в виді дробу 4/4". Якщо ваш школяр зрозумів даний концепт, переходьте до інших цілих дробів. Розділіть печиво на 2, 3 і 5 частин, продовжуючи вивчення.
Коли число зверху у дробі становить половину нижнього, то дріб можна представити як 1/2.
Половину можна виразити у формі дробів за різними варіантами. Поясніть, що 2/4, 4/8 і 6/12 у всіх випадках вказують на половину числа, і всі ці дроби можна спростити до 1/2. Для визначення, чи можливо дріб виразити як 1/2, необхідно поділити знаменник на чисельник. Якщо ми отримаємо в результаті число 2, то дріб дорівнює ½ у всіх випадках.
Якщо чисельник у дробі перевищує нижнє, то дріб вважається "неправильним".
Важливо дати зрозуміти, що тут термін "неправильний" не означає помилковість, а лише вказує на специфіку такого дробу. Щоб зробити це зрозумілішим, порівняйте дріб 9/3 з "тяжким дробом", який хоче скинути вагу. "Чисельник заважкий, тому знаменнику важкувато его утримувати. Щоб зменшити вагу, його потрібно зменшити, тобто 9 треба поділити на 3".
Як допомогти дитині зрозуміти віднімання та додавання дробів?
Після того, як школяр освоїв, що таке "дріб", переходьте до виконання арифметичних операцій з дробами. Почніть з найпростіших випадків додавання дробів зі спільним або однаковим знаменником. Поясніть: "Коли додаємо дроби, обережно слідкуй за знаменником. Коли він один і той самий в дробах, просто додайте чисельників. Наприклад, 2/8 + 4/8 = 6/8".
Той самий принцип застосовується й до віднімання: "При відніманні також подивиться на знаменник. Якщо він спільний, просто відніміть чисельники. Наприклад, 5/7 – 2/7 = 3/7".
У випадку відсутності в дробах спільний знаменника, треба його відшукати. Спільним називається знаменник, який можна розділити і на один, і на інший знаменник дробів. Давайте з'ясуємо, як розповісти про це дитині: "Коли ми хочемо додати 2/3 та 5/6 і відсутній спільний знаменник, ми вибираємо знаменник другого дробу як спільний, тобто 6. 6 можна розділити і на 6, і на 3. Тепер нам треба перетворити 2/3 так, щоб його знаменник був 6. Збільшивши обидва числа вдвічі, отримаємо 4/6. Тепер можна додати 4/6 + 5/6 як було описано вище".
Декілька корисних порад для ефективного пояснення дробів дітям
- Використовуйте їжу та різні предмети
Запропонуйте гру з дробами, використовуючи фрукти, торт, лего, мозаїку чи звичайний папір. Підберіть предмети, які найбільше зацікавлять вашу дитину. - Практикуйте візуальне представлення дробів через малюнки
Діти чудово розуміють інформацію, виражену візуальними засобами. Можете створювати малюнки, на яких ви ділите намальоване на частини та зафарбовуєте декілька з них. Приміром, можна створити чи роздрукувати зображення кола, яке розділене за допомогою ліній на декілька частин. Запропонуйте дитині малювати кілька таких фігур і поставте питання, який дріб отримали. Якщо вона замалювала, наприклад, 2 із 4 частин, то вийде дріб 2/4. - Будьте терплячими
Іноді для дітей розуміння складних тем з деяких шкільних предметів потребує більших зусиль. До таких тем відносяться дроби, вони можуть викликати складнощі у школярів, і саме тому їх вивчення надзвичайно важливе. Важливо пам'ятати, що коли дитина усвідомлює, що вона може впоратися із складною темою, це стане для неї важливим кроком у подоланні інших труднощів у навчанні. Головний урок, який дитина повинна засвоїти, полягає в тому, що за допомогою практики і наполегливості можна освоїти навіть найскладніші, на перший погляд, теми.
В такі моменти важливо для батьків виявити терпіння та утриматися від тиску, уникаючи висновків щодо здібностей дитини. Якщо їй складно зрозуміти дроби, це не свідчить про її обмеженість в галузі точних наук. Замість цього, це може вказувати на те, що їй просто потрібен додатковий час для освоєння матеріалу та підтримки від батьків чи репетиторів.